프림 알고리즘(Prim Algorithm) 구현과 증명

프림 알고리즘(Prim Algorithm)이란?

어떠한 그래프에서 최소신장트리(Minimum Spanning Tree)를 찾는 알고리즘이다.

그리디(Greedy) 알고리즘 중 하나이다.

 

프림 알고리즘(Prim Algorithm)의 아이디어

• 트리중 하나의 노드에서 시작(아무 노드나 상관없음)
• 우리가 만들어가고 있는 트리에 인접한 edge들 중 가장 작은 weight를 가진 edge를 추가
• (단, 사이클을 만들지 않아야함)
• spanning tree가 될때까지 반복 

  

  출처 : https://en.wikipedia.org/wiki/File:Prim-animation.gif

프림 알고리즘(Prim Algorithm)의 증명

정확성

G : 주어진 그래프(방향성X, 가중치O)

V : 전체 node의 집합

E : 전체 edge의 집합

Y : 방문한 node

F : 방문한 edge

 

G = (V,E)로 나타낼 수 있고, F ⊆  E, Y ⊆ V이다.

G'(만들어가는중인 그래프) = (Y,F)

MST = (V,F') 이라고 정의하자.

 

가장 처음 F는 empty set이므로 F ⊆ F' 이 성립한다. 

 

1. G'에 인접한 edge들 중 가장 가중치가 낮은 edge를 e(v1 ∈ Y와 v2 ∈ V-Y를 잇는 edge)라고 하자

2. e가 F'의 원소일 경우, F U {e} 도 MST가 될 수 있는 상태이다.

3. e가 F'의 원소가 아닐 경우, F'은 spanning tree이므로 F' U {e}에는 하나의 사이클이 생길것이다.

    이때, F' U {e}에는 사이클에 속하지만 F에 속하지 않는 edge e'가 존재할 것이다.

3-1. F' U {e} - {e'}이 spanning tree가 된다면 e<=e'이므로, F' U {e} - {e'} 이 MST일 것이다.

3-2. F U {e} ⊆ F' U {e} - {e'} 이므로 F U {e}는 항상 MST가 될 수 있는 상태이다.

 

이를 Y=V가 될 때까지 반복하여 MST를 만들 수 있다.

 

시간복잡도

E = edge, V = vertex

Minimum edge weight data structure	Time complexity (total)
adjacency matrix, searching	$O(|V|^2)$
binary heap and adjacency list	$O((|V|+|E|)log|V|) = O(|E|log|V|)$
Fibonacci heap and adjacency list	$O(|E|+|V|log|V|)$

출처 : https://en.wikipedia.org/wiki/Prim%27s_algorithm

구현(백준 1647번)

문제

동물원에서 막 탈출한 원숭이 한 마리가 세상구경을 하고 있다. 그러다가 평화로운 마을에 가게 되었는데, 그곳에서는 알 수 없는 일이 벌어지고 있었다.

마을은 N개의 집과 그 집들을 연결하는 M개의 길로 이루어져 있다. 길은 어느 방향으로든지 다닐 수 있는 편리한 길이다. 그리고 각 길마다 길을 유지하는데 드는 유지비가 있다. 임의의 두 집 사이에 경로가 항상 존재한다.

마을의 이장은 마을을 두 개의 분리된 마을로 분할할 계획을 가지고 있다. 마을이 너무 커서 혼자서는 관리할 수 없기 때문이다. 마을을 분할할 때는 각 분리된 마을 안에 집들이 서로 연결되도록 분할해야 한다. 각 분리된 마을 안에 있는 임의의 두 집 사이에 경로가 항상 존재해야 한다는 뜻이다. 마을에는 집이 하나 이상 있어야 한다.

그렇게 마을의 이장은 계획을 세우다가 마을 안에 길이 너무 많다는 생각을 하게 되었다. 일단 분리된 두 마을 사이에 있는 길들은 필요가 없으므로 없앨 수 있다. 그리고 각 분리된 마을 안에서도 임의의 두 집 사이에 경로가 항상 존재하게 하면서 길을 더 없앨 수 있다. 마을의 이장은 위 조건을 만족하도록 길들을 모두 없애고 나머지 길의 유지비의 합을 최소로 하고 싶다. 이것을 구하는 프로그램을 작성하시오.

입력

첫째 줄에 집의 개수 N, 길의 개수 M이 주어진다. N은 2이상 100,000이하인 정수이고, M은 1이상 1,000,000이하인 정수이다. 그 다음 줄부터 M줄에 걸쳐 길의 정보가 A B C 세 개의 정수로 주어지는데 A번 집과 B번 집을 연결하는 길의 유지비가 C (1 ≤ C ≤ 1,000)라는 뜻이다.

임의의 두 집 사이에 경로가 항상 존재하는 입력만 주어진다.

출력

첫째 줄에 없애고 남은 길 유지비의 합의 최솟값을 출력한다.

예시

 

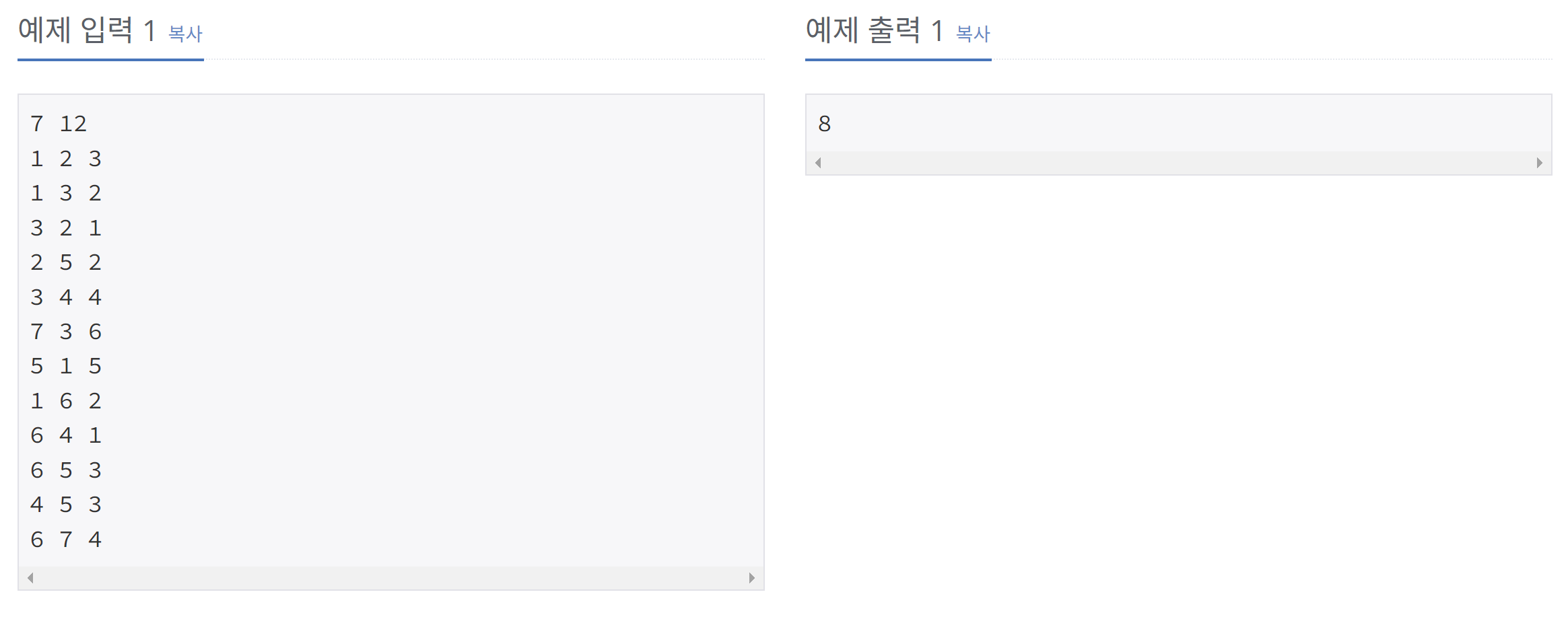
풀이

MST를 구하는 문제로, kruskal알고리즘 또는 Prim 알고리즘을 사용할 수 있다. 이 글에선 Prim알고리즘을 사용하여 문제를 풀어보았다.

입력받은 값들로 MST를 구한 후 가장 긴 edge를 제거하면 풀리는 문제이다.

#include <iostream>
#include <queue>
#include <vector>

using namespace std;

typedef struct edge {
    int vertex1, vertex2;
    int weight;

    edge() {
        vertex1 = 0;
        vertex2 = 0;
        weight = 0;
    }

    edge(int v1, int v2, int w) {
        vertex1 = v1;
        vertex2 = v2;
        weight = w;
    }

    bool operator < (const edge& e) const {
        return weight < e.weight;
    }
}edge;

int Prim(int* vertex, vector<edge> edges[], int v) {
    int total_weight = 0;
    priority_queue<edge> adj_edges;
    int cur_vertex = 0, max_edge=0;
    vertex[0] = 1;

    for (int j = 0; j < v - 1; j++) {
        for (int i = 0; i < edges[cur_vertex].size(); i++) {
            adj_edges.push(edges[cur_vertex][i]);
        }
        while (!adj_edges.empty() && (vertex[adj_edges.top().vertex1] == 1 && vertex[adj_edges.top().vertex2] == 1)) {
            adj_edges.pop();
        }
        edge e = adj_edges.top();
        adj_edges.pop();
        vertex[e.vertex2] = 1;
        cur_vertex = e.vertex2;
        total_weight += e.weight;
        if(max_edge>e.weight){
            max_edge = e.weight;
        }
    }
    // return MST; 이렇게 하고 싶지만 최대한 빠르게 하기 위해서..total_weight를 리턴하는 걸로 하자
    return  -(total_weight-max_edge);

}

int main()
{
    int v, e;
    int v1, v2, w;
    int total_weight = 0;

    scanf("%d %d", &v, &e);

    int* vertex = new int[v];
    fill(vertex, vertex + v, 0);
    vector<edge> *edges = new vector<edge> [v];

    for (int i = 0; i < e; i++) {
        scanf("%d %d %d", &v1, &v2, &w);
        edges[v1-1].push_back(edge(v1-1, v2-1, -w));
        edges[v2-1].push_back(edge(v2-1, v1-1, -w));
    }

    total_weight = Prim(vertex, edges, v);
    printf("%d\n", total_weight);
}

 

 

 

오류수정은 언제나 환영입니다^^